04.17
MLOps
쿠버네티스는 왜 쓰는가??
- 인스턴스 컨테이너를 1000개 이상 띄울 경우에는 유용, 하지만 너무 복잡
- 작게 띄울 때는 도커 스웜만으로도 충분, 도커만 설치하면 자동으로 깔려서 구현도 편하고 다룰 컨테이너가 적을 경우에는 용이
- 요즘은 k3s 같은 경량화 툴이 많이 나와서 비교적 편리해진 편 + 산업계의 표준이 돼버려서 배울 필요는 있을듯..?
- mlops 0단계 구현할 때는 필요 없다고 한다
MLflow 튜토리얼: https://github.com/vhrehfdl/MLflow_tutorial
04.19
확률과 통계
이산형 확률분포
- 단순임의추출법(simple random sampling)
- 크기가 $N$개인 유한모집단에서 크기$n$의 표본을 추출하는 방법의 수는 $_NC_n$
- $_NC_n$에서 모든 경우가 동일한 확률로 뽑힐 때 단순임의추출법
이항 분포(binomial distribution)
- n번의 독립적인 베르누이 시행
- 베르누이 시행: 시행의 결과가 2개고 상호배반, 각 시행이 서로 독립일 경우
- 확률변수 $X$: $n$번의 시행에서 성공한 횟수
- $n$: 시행 횟수
- $p$: 확률
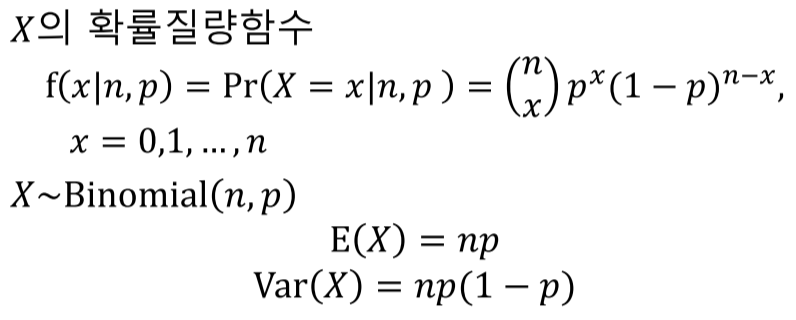
- 순열(permutation): 순서를 고려
- 조합(combination): 순서 고려x
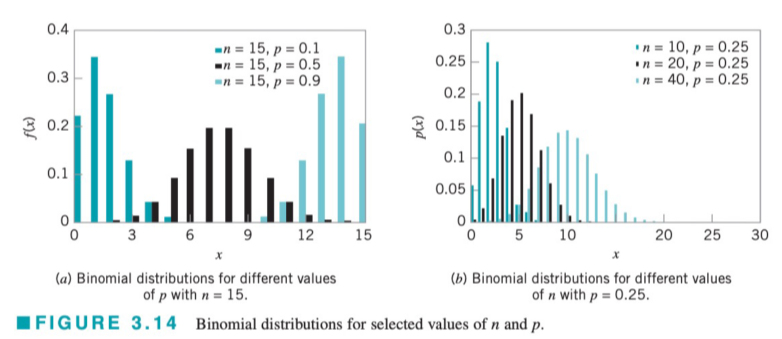
- n이 고정일 때, p=1/2에 가까울수록 그래프가 좌우대칭
- p가 고정일 때, n이 커질수록 그래프가 좌우대칭
초기하 분포(Hypergeometric distribution)
- 크기가 $N$인 유한모집단에서 $M$개는 특별한 속성, 나머지 $N-M$개는 속성을 갖고있지 않을 경우
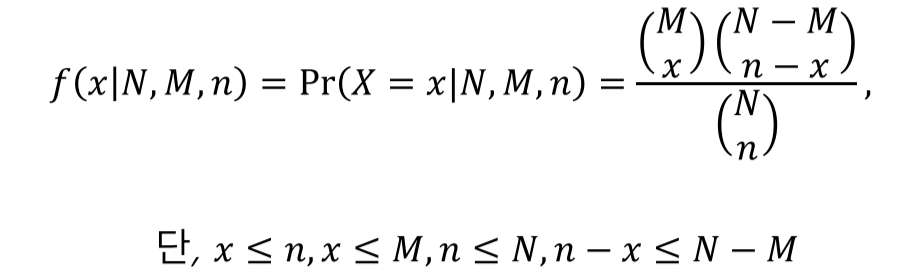
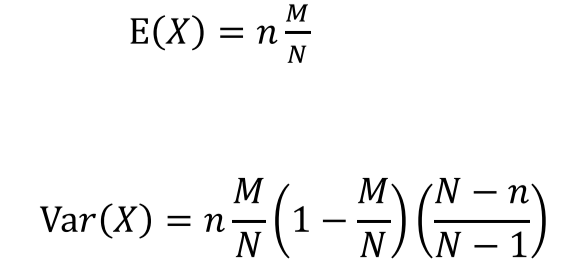
포아송 분포(Poisson distribution)
- 확률변수 $X$: 단위구간(일정한 시간, 거리, 면적, 무게 등)에서 관심의 사건이 일어나는 횟수가 다음 가정을 만족할 경우 $X$는 푸아송 분포
- 사건은 구간에서 무작위
- 단위구간에서 2번 이상 사건이 일어날 확률은 0
- 사건이 일어날 확률은 모두 같다
- 한 구간에서의 사건은 다른 구간에서의 사건과 독립
- $X$의 확률질량함수
- $\mu$: 기대값, 평균, E(x)
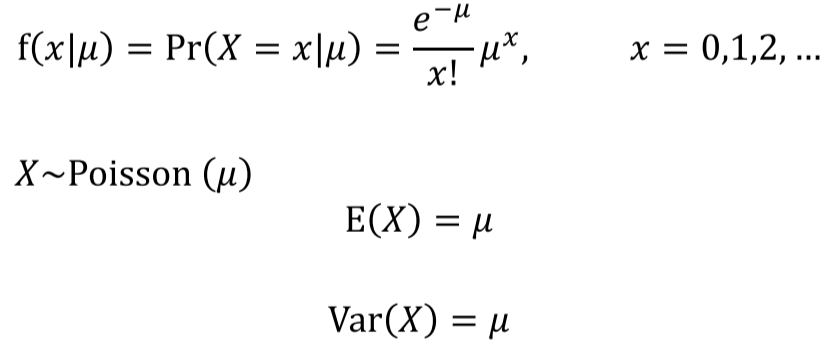
04.20
확률과 통계
연속형 확률분포
균등분포
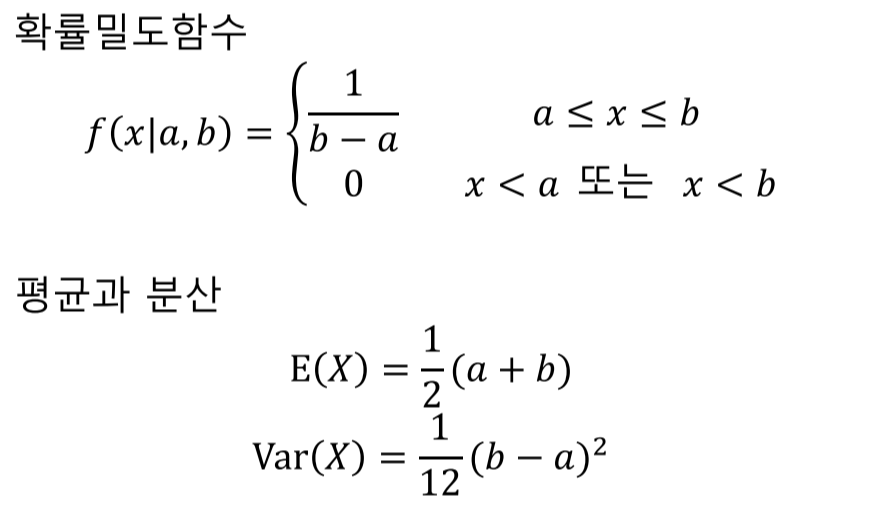
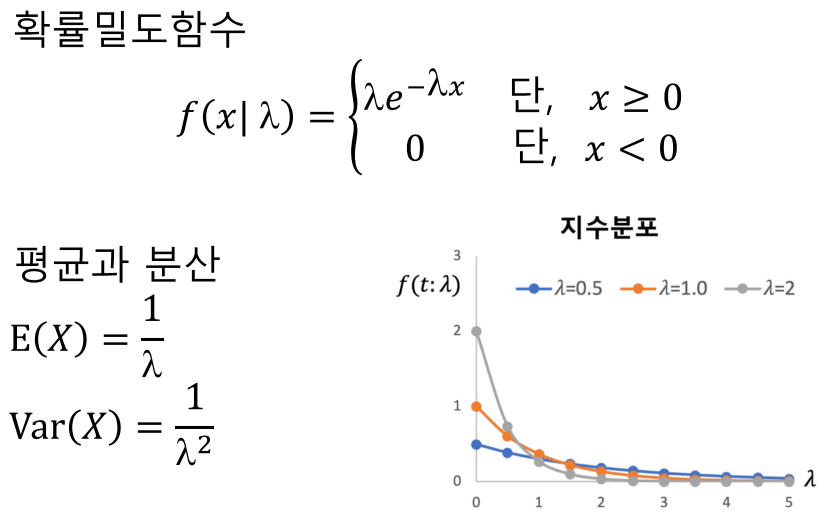
지수분포
정규분포

$\mu$는 중심, $\sigma$는 퍼진 정도를 결정
표준정규분포(Standard normal distribution): 평균이 0, 표준편차가 1인 정규분포
- 정규분포의 성질
- $X \sim N(\mu, \sigma^2)$일 때 임의의 상수 a,b에 대해 $aX+b \sim N(a\mu+b, a^2\sigma^2)$가 성립
- 따라서 모든 정규분포는 표준정규분포로 변환해 확률값을 계산할 수 있음
- $X_1 \sim N(\mu_1, {\sigma_1}^2)$이고 $X_2 \sim N(\mu_2, {\sigma_2}^2)$이며 $X_1, X_2$가 서로 독립이라면 $Y = X_1 + X_2 \sim N(\mu_1+\mu_2, {\sigma_1}^2+{\sigma_2}^2)$
- 만약 $X_i \sim N(\mu, \sigma^2)$(identically normal)이고, $1 \leq i\leq n$이며 서로 독립(independent)라고 하면, 표본평균 $\bar{X}=\frac{\sum_{i=1}^{n} X_{i}}{n}$의 분포는 $\bar{X} \sim N(\mu, \sigma^2/n)$(i.i.d)
- 이항분포의 정규분포 근사
- $X \sim Binomial(n,p)$일 때 $\frac{(X-n p)}{\sqrt{n p(1-p)}}$는 근사적으로 표준정규분포를 띈다
- 여기서 0.5는 연속화 보정
- 일반적으로 근사화는 $np\geq5$이며, 큰 값일수록 정확해짐
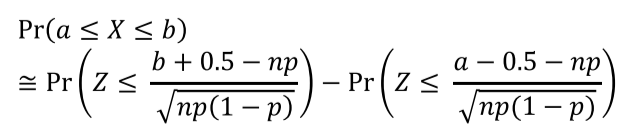
'개발 및 공부 > Today I Learned' 카테고리의 다른 글
| TIL) 22.05.01 ~ 22.05.07 (0) | 2022.05.03 |
|---|---|
| TIL) 22.04.10 ~ 22.04.16 (0) | 2022.04.12 |
| TIL) 22.04.03 ~ 22.04.09 (0) | 2022.04.04 |
| TIL) 22.03.27 ~ 22.04.02 (0) | 2022.03.27 |
| TIL) 22.03.25 ~ 22.03.26 (0) | 2022.03.26 |