04.10
졸작
matlab 그래프 사이즈 설정:
plt.figure(figsize=(30,30))이미지 저장:
plt.savefig(result_folder + '/' + str(imgid) + '.png')json 파일 다루기
# 열기 with open(orig_file, 'r') as f: orig_json = json.load(f)# 저장 with open(output_file, 'w') as f: json.dump(output_json, f)
04.12
졸업작품 관련
- 좀비 프로세스 죽이기
원인: train.py 돌리다가 ctrl+c가 아니라 ctrl+z를 눌러서 제대로 종료되지 않았던 문제
해결:ps -ef로 부모 프로세스를 찾아 삭제
https://zetawiki.com/wiki/%EC%95%88_%EC%A3%BD%EB%8A%94_%EC%A2%80%EB%B9%84_%ED%94%84%EB%A1%9C%EC%84%B8%EC%8A%A4_%EC%A3%BD%EC%9D%B4%EA%B8%B0 - wandb 사용하기
https://greeksharifa.github.io/references/2020/06/10/wandb-usage/#wandbinit
https://www.programcreek.com/python/example/121966/wandb.init
https://velog.io/@hanlyang0522/%EC%9D%B4%EB%AF%B8%EC%A7%80-%EB%B6%84%EB%A5%98-%EA%B3%BC%EC%A0%9C-%EC%9D%B4%EC%8A%88#wandb COCOeval.evaluate()결과값 저장
COCOeval.summarize()로는 결과가 출력만 되고 저장되지 않아 코드 뜯어보니 summarize()는 COCOeval.stats을 출력return COCOeval.stats로 해결
04.16
확률과 통계
확률분포
- 확률변수(random variable): 확률실험의 결과에 실수 값을 대응시켜주는 함수
- 반복된 실험에서 그 값이 변하는 수치 변수(numerical variable)
- i.e. 임의로 진행되는 실험(동전을 던지는 실험)에서 일정한 확률(앞1/2, 뒤1/2)을 갖고 발생하는 결과에 실수 값(앞:1, 뒤:0)을 부여하는 변수(variable)
- 확률분포(probability distribution): 확률변수의 분포, 즉 확률변수가 어떤 값을 취하며 그 값을 얼마나 자주 취하는지 보여주는 표나 수식, 그림
- 이산형: 확률질량함수
- 연속형: 확률밀도함수
- 이산형 확률분포: 확률변수 X의 가능한 값에 각각 확률을 할당
- 확률변수 $X$의 값에 따른 확률값 $P(X=x_i)$를 대응시키는 함수 $X$를 확률질량함수(probability mass function, pmf)라고 부름
- 확률질량함수: $f(x_i) = P(X=x_i)$, $x_i$는 실제 실험값
- 누적분포함수(cumulative distribution function, cdf): $F(x) = P(X\le x)$
- 연속형 확률분포: 확률밀도함수(probability density function, pdf)
- X가 가질 수 있는 값이 무수히 많기 때문에 특정 값을 취할 확률 = 0, $P(X=a) = 0$
- 누적분포함수(cdf): $F(x)=\operatorname{Pr}(X \leq x)=\int_{-\infty}^{x} f(y) d y$
기대값
- 기대값(expected value): 확률변수의 평균
- 이산형
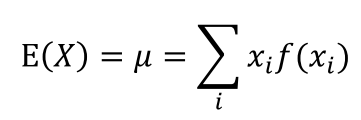
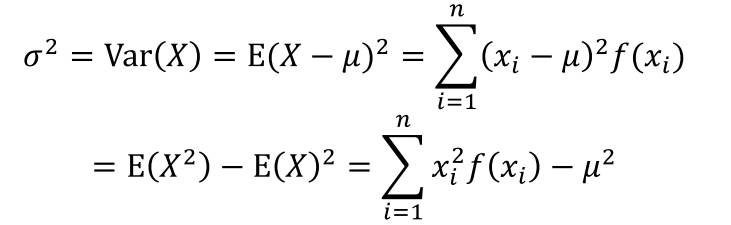
- 연속형
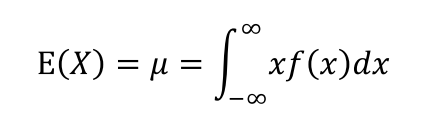
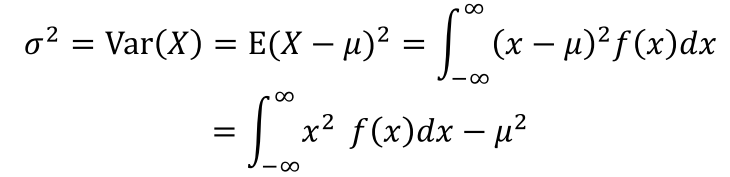
결합확률분포(joint probability distribution): 2개 이상의 확률변수가 동시에 관측된 경우 이들이 동시에 취하는 여러 가지 값들에 확률을 대응시켜주는 관계
이산형: 결합확률질량함수(joint pmf), 결합누적분포함수(joint cdf)
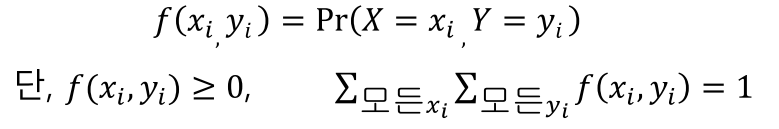
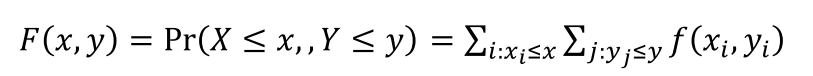
- 연속형: 결합확률밀도함수(joint pdf), 결합누적분포함수(joint cdf)
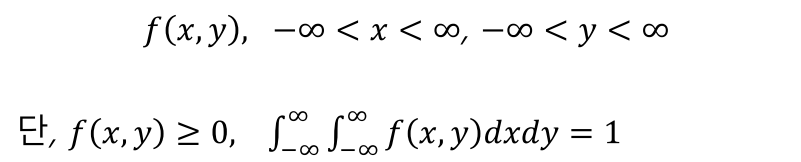
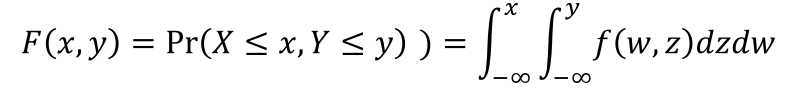
- 주변확률분포(marginal probability distribution): 결합분포에서 얻은 한 확률변수, 나머지 확률 변수를 모든 값으로 두고 구할 수 있다

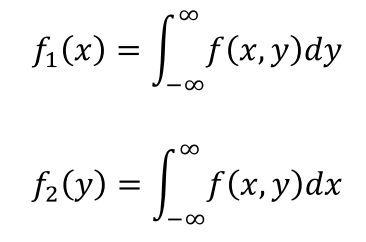
- 공분산(covariance)
- 분산과 달리 음수도 나올 수 있다
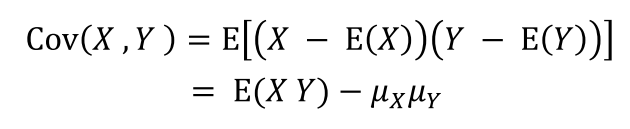
- 상관계수(correlation coefficient)
- $Corr(X,X)=1$, 자기와의 상관관계는 1
- 항상 -1~1 사이의 값을 갖는다
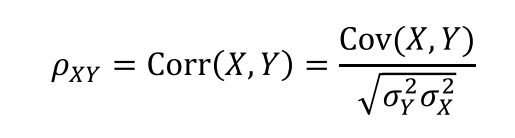
- 공분산과 상관계수의 성질

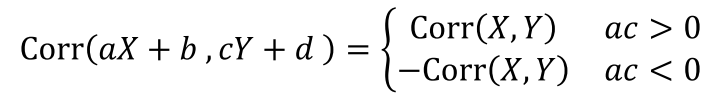
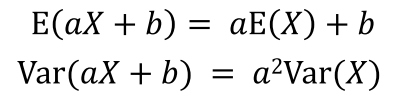
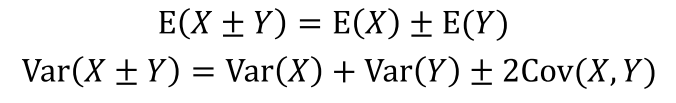
- 확률변수의 독립성: 확률변수 $X$와 $Y$의 결합분포에서 모든 $(x_i,y_i)$에 대해 $f(x_i,y_i) = f_1(x_i)f_2(y_i)$일 경우 두 확률변수가 독립
- $X$와 $Y$가 독립일 때 공분산은 0이고 상관계수도 0이다. 하지만 그 역은 성립하지 않음
'개발 및 공부 > Today I Learned' 카테고리의 다른 글
| TIL) 22.05.01 ~ 22.05.07 (0) | 2022.05.03 |
|---|---|
| TIL) 22.04.17 ~ 22.04.23 (0) | 2022.04.17 |
| TIL) 22.04.03 ~ 22.04.09 (0) | 2022.04.04 |
| TIL) 22.03.27 ~ 22.04.02 (0) | 2022.03.27 |
| TIL) 22.03.25 ~ 22.03.26 (0) | 2022.03.26 |