03.25
선형대수
선형변환(Linear Transformation)
- 정의: $T(cu+dv) = cT(u)+dT(v)$일 경우 $T$는 linear transformation
- 행렬곱으로 나타낼 수 있다면 항상 선형변환
- 선형변환은 벡터를 표현하는 좌표계를 변형하는 연산
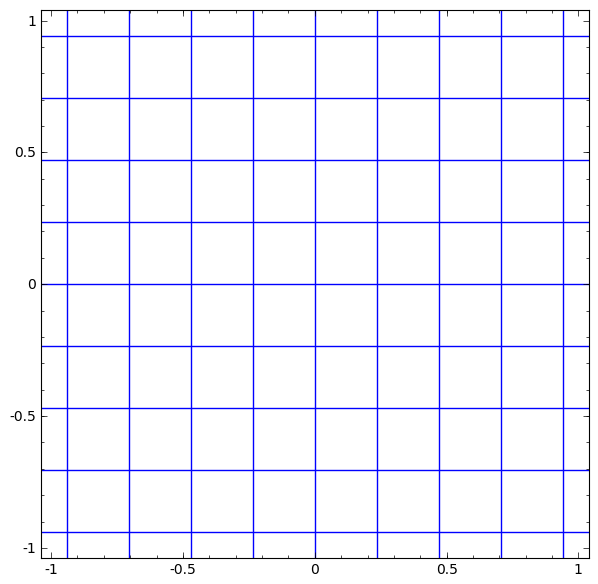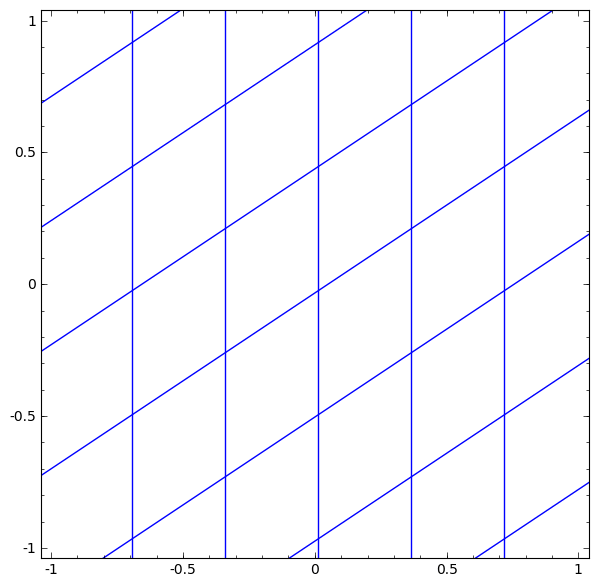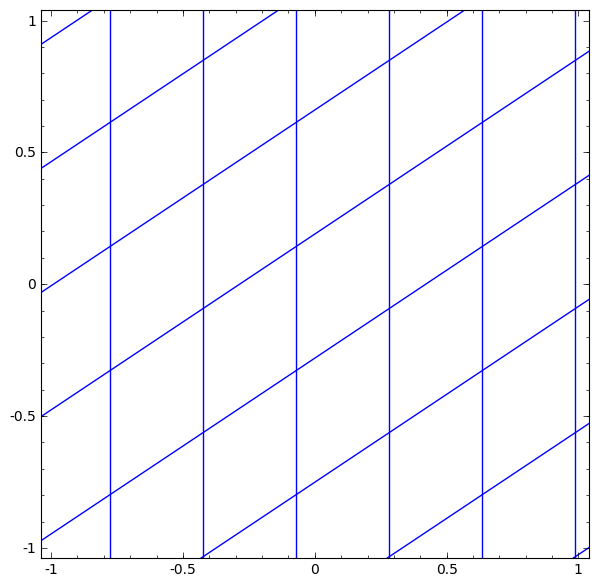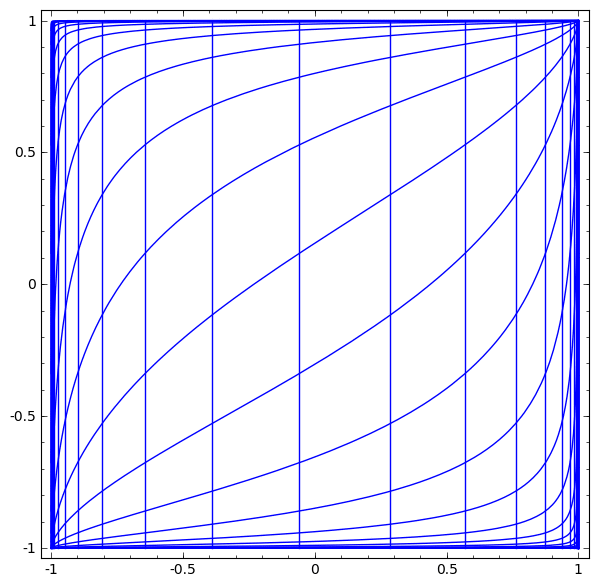
- Affine transform은 bias 때문에 linear transform이 아닌데 벡터 마지막에 1을 추가해 linear하게 만들 수 있다

전사함수, 일대일대응
- onto: 전사(전체로 사형)하다, 전사하는 함수를 전사함수라고 표현
공역==치역일 경우
정의역의 개수 >= 공역의 개수일 경우 가능성 0 - $T:R^n -> R^m$에서 $n<m$일 경우 전사하지 못한다 == NN에서 input dim이 작아 공역 전체를 덮지 못한다? 표현하기 어렵다? == 정보손실 발생
- one-to-one: 일대일 대응
linearly independent한 경우에만 가능
$T:R^n -> R^m$에서 $n<m$일 경우 one-to-one 불가능 - -> Input보다 output의 차원이 낮아 dependent할 경우 한 결과값에 대해 여러 해가 존재하기 때문에 one-to-one이 불가능
Least-square problem
- Over-determined linear problems: 미지수보다 방정식이 많으면 보통 해가 존재하지 않음(적은 수의 벡터로 만들 수 있는 span에 모든 벡터가 들어올 가능성이 희박)
이를 근사(approximately obtain)하기 위해 least squre를 사용

- Least square solution은 error( $||b-Ax||$ )를 최소화하는 x를 찾는 문제
- b: Ground truth
- Ax: estimated output

- 기하학적 의미로는 solution $b$와 가장 거리가 가까운 $\hat{b}$를 찾는 작업
$\hat{b}$은 b와 가장 가까운 점이기 때문에 $b$와 $\hat{b}$를 이은 직선은 Col A(subspace, span, A로 만들 수 있는 평면?)에 수직(수직이 최단거리) - 따라서 A 위의 모든 벡터는 모두 $b-\hat{b}(Ax)$에 수직

- Normal equation: $Ax≃b$를 푸는 문제는 결국 $A^TA\hat{x}=A^Tb$ 를 푸는 것과 동일해 진다
$A^TA$가 역행렬이 있다면 $\hat{x}$를 구할 수 있음

03.26
Pose Estimation
Fast Human Pose Estimation
- 논문
- 구현
- Computation, model size 줄이기와 performance 높이기에 집중
- 이를 해결하기 위해 Fast Pose Distillation이라는 기법을 제시
- lightweight hourglass network 사용: 기존 hourglass를 절반으로 줄임
- SOTA hourglass로 teacher network 학습
- Knowledge distillation 사용, teacher network를 보고 student network가 추론

- 결과는 heatmap으로 나와 정확한 값은 나오지 않음

다른 SOTA와 성능차이가 거의 나지 않음

COCO dataset엔 hrnet을 backbone으로 사용

HigherHRNet
- 논문
- 구현
- Bottom-up 방식은 정확도가 낮고 scale에 따라 영향을 많이 받음
특히 작은 scale일수록 정확도가 매우 낮음 - Image pyramid는 1/4 ~ 1/32 크기에서 예측해야 되기 때문에 bottom-up 방식에는 적합하지 않음
- 이를 개선하기 위해 1/4 정도의 고화질 pyramid feature만 사용해 고화질 heatmap을 생성

- Backbone은 HRNet을 사용하고 deconv로 1/2 feature map을 생성
- 처음부터 1/2 feature map을 만들면 computation이 너무 커져 처음엔 HRNet으로 1/4를 사용

'개발 및 공부 > Today I Learned' 카테고리의 다른 글
| TIL) 22.05.01 ~ 22.05.07 (0) | 2022.05.03 |
|---|---|
| TIL) 22.04.17 ~ 22.04.23 (0) | 2022.04.17 |
| TIL) 22.04.10 ~ 22.04.16 (0) | 2022.04.12 |
| TIL) 22.04.03 ~ 22.04.09 (0) | 2022.04.04 |
| TIL) 22.03.27 ~ 22.04.02 (0) | 2022.03.27 |